Small Open Economy Extension (IRBC)

Macro II - Fluctuations - ENSAE, 2024-2025

Author

Pablo Winant

Published

March 19, 2025

Introduction and Basic Facts

Why a small open economy?

What are the classical reasons to open economy to trade?

trade integration
- taste for variety
- comparative advantage
financial integration
- smooth shock / insurance

From RBC to IRBC

RBC models have been very successful at matching Business Cycles

(temporary) victory against keynesian view that short term fluctuations result from demand shocks
so successful that facts at odd with theoretical predictions have been called “puzzles”

. . .

It didn’t take long before the same methodology was applied to International Business Cycles

. . .

Seminal Paper:

International Real Business Cycles, Backus, Kehoe, Kydland (1992) (freshwater economists)

Very successful methodology:

facts at odd with theoretical predictions have been called “puzzles”

IRBC Facts

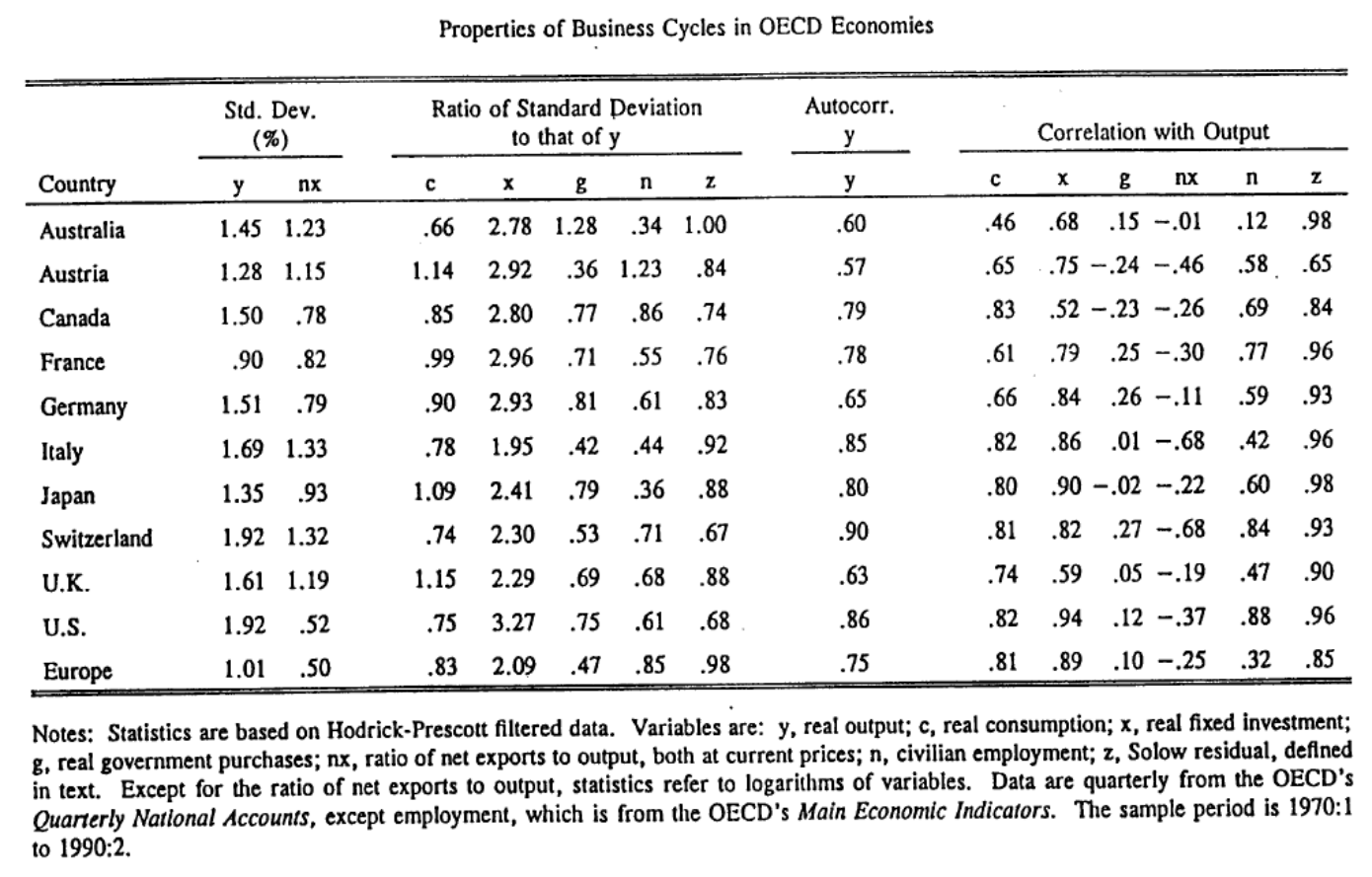
From Kehoe,Kydland (1995)

IRBC Facts

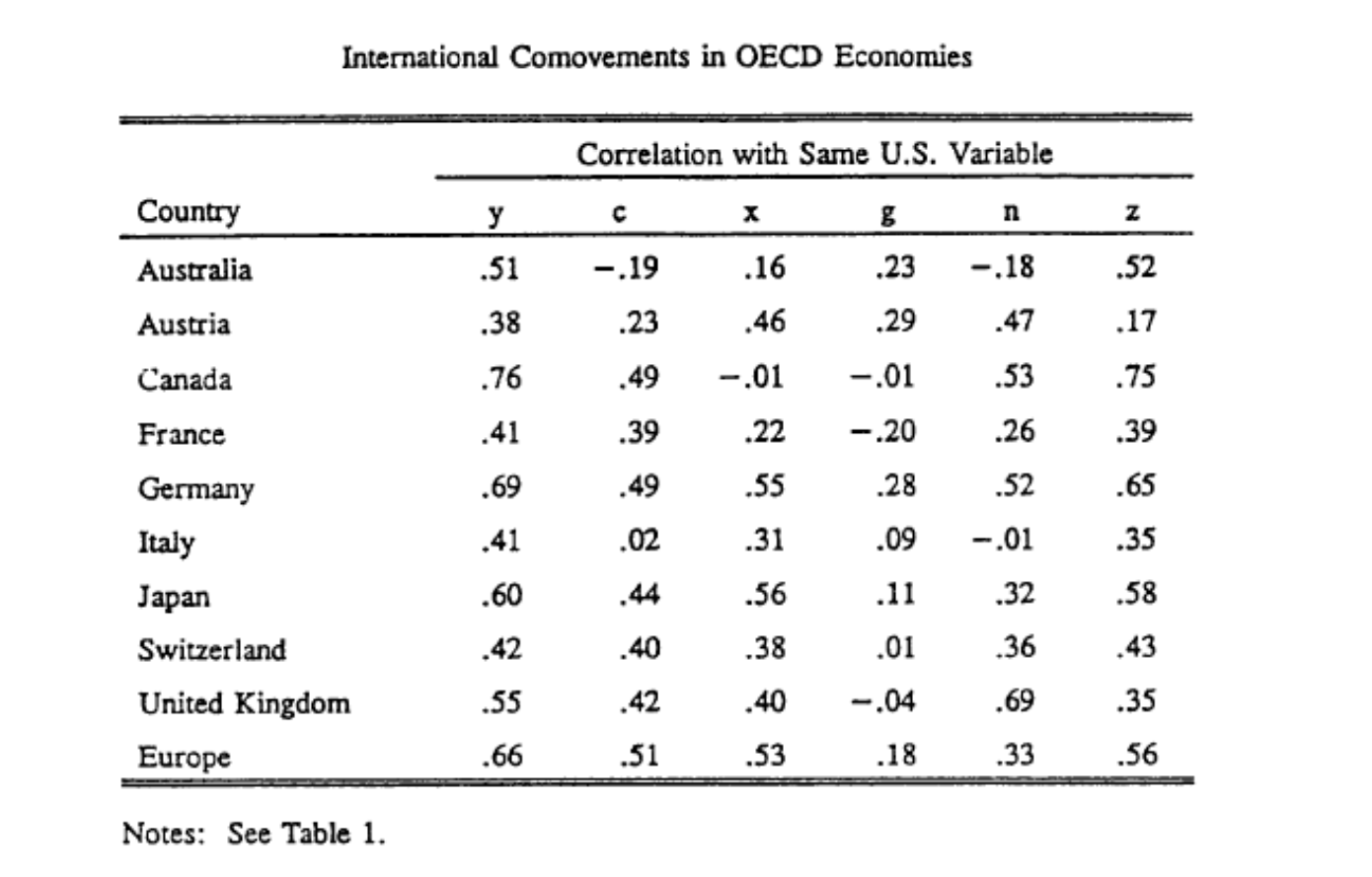
Stylized Facts

Domestically:

output more variable than consumption
output autocorrelated
productivity strongly procyclical
trade balance strongly countercyclcal
positive comovements in output

Internationally:

smaller comovements in consumption
- Backus-Kehoe-Kydland puzzle

. . .

Can we replicate these moments with a BC model?

Modeling a Small Open Economy

Endowment model

Representative agents maximizes: \[\max_{c_t} \sum_{t=0}^{\infty} \beta^t u(c_t)\] \[c_t + a_{t} \leq y_t + (1+r) a_{t-1} \]

Endowment economy:

income \((y_t)_t\) is exogenously given
for simplicity we assume it is deterministic

Small open economy:

open: can save \(a_t\) which yields \(a_{t+1}(1+r)\) in the next period
small: country takes world interest rate \(r\) as given (no effect on world prices)

We solve this problem with the terminal conditions:

\(a_{-1}\) given¹
\(\lim_{T\rightarrow\infty} \frac{a_{T}}{(1+r)^T}\geq0\)
- no-ponzi condition

The no-ponzi condition will in effect eliminate diverging solutions.

In a first order approximation, it selects the right eigenvalues.

Endowment model (3)

We get the lagrangian:

\[\mathcal{L}= \sum_{t=0}^{\infty} \beta^t u(c_t) + \sum_{t=0}^{\infty} \beta^t \lambda_t \left(y_t + (1+r) a_{t-1} - c_t-a_{t} \right)\]

First order conditions:

\[\begin{align} u^{\prime}(c_t)& =& \lambda_t \\ \lambda_t &=& \beta (1+r) \lambda_{t+1} \end{align}\]

Under the technical assumption \(\beta (1+r)=1\) we get \(c_t=c_{t+1}\) then

\[c_0 = \frac{r}{1+r}\left\{ (1+r) a_{-1} + \sum_{t=0}^{\infty} \frac{y_t}{(1+r)^t}\right\}\]

. . .

consumption is determined by permanent income
- changes in initial wealth have permanent effects
remark: problem isomorphic to consumption-savings decisions

Current Account

Reminders on Current Account

The trade balance is exports-imports (here \(y_t-c_t\))

The current account is trade balance + net factor payments (here \(y_t-c_t+r a_{t-1}\))

Positive current account: additional lending to the rest of the world.

. . .

Using the formula from before

\[CA_0 = a_{-1} r + (1-\frac{r}{1+r}) y_0 - \frac{r}{1+r}\left\{ \sum_{t\geq1}^{\infty} \frac{y_t}{(1+r)^t}\right\}\]

How does the current account reacts to income shocks?

current account responds positively to temporary shock in income
and to news about future income shocks:
- This is the intertemporal approach to the current account

Unit root

Still with the same formula: \[c_0 = \frac{r}{1+r}\left\{ (1+r) a_{-1} + \sum_{t=0}^{\infty} \frac{y_t}{(1+r)^t}\right\}\]

What is the effect of an increase in \(a_{-1}\)?

- consumption rises permanently
- $a_t$ is constant, equal to $a_{-1}$
- agent consumes small amount $r$ corresponding to interests paid forever on $a_{-1}$

this will correspond to a unit root in the solution

Adding capital

We add capital and production to our endowment economy: \[y_t = z_t k_{t-1}^\alpha\] \[k_t = (1-\delta) k_{t-1} + i_{t}\]

The aggregate resource constraint becomes:

\[a_{t} + c_t + i_t = (1+r) a_{t-1} + y_t\]

Now maximize \(\sum_t \beta^ t U(c_t)\)

. . .

We get first order conditions

\[\lambda_t = \beta \lambda_{t+1} (1+r)\] \[\lambda_t = \beta \lambda_{t+1}\left[ (1-\delta) + z_{t+1} f^{\prime}(k_{t}) \right]\]

where \(\lambda_t\) is lagrange multiplier associated to budget constraint.

Adding capital: optimality conditions

Since \(\lambda_t>0\) (constraint is always binding), we get:

\[(1-\delta) + z_{t+1} f^{\prime}(k_{t}) = 1+r\]

\[k_{t} = \left( \frac{r+\delta}{\alpha z_{t+1}}\right)^{\frac{1}{\alpha-1}}\]

and investment \[i_t = \left( \frac{r+\delta}{\alpha z_{t+1}}\right)^{\frac{1}{\alpha-1}}- (1-\delta)\left( \frac{r+\delta}{\alpha z_{t}}\right)^{\frac{1}{\alpha-1}}\]

. . .

Here investment is fully determined by productivity shocks

too simple: no international dependence

Add friction to the investment

A possible solution: change the resource constraint such that adjusting capital is costly

For instance:

\[a_{t} + c_t + i_t + \frac{\omega}{2}\frac{(k_{t}-k_{t-1})^ 2}{k_t} = (1+r)a_{t-1} + z f(k_{t-1})\]

\[k_{t} = (1-\delta) k_{t-1} + i_t\]

where \(\omega\) is an adjustment friction.

. . .

Typically, \(\omega\) is chosen so that the model replicates \(\frac{Var(i_t)}{Var(y_t)}\) from the data.

. . .

🔜 Cf tutorial.

A benchmark Small Open Economy Model

Stephanie Schmitt Grohe and Martin Uribe

Closing Small Economy Models, Schmitt Grohe and Uribe (2003), JIE

small open economy model with production, consumption-leisure tradeoff and capital adjustment costs
- = RBC+open+adj costs
perform some moments matching
compare different ways of stationarizing

The model

\[\max_{c_t, n_t} \sum_{t=0}^{\infty} \beta^t u(c_t, n_t)\]

\[c_t + k_{t} + a_{t} = y_t + g_t - \frac{\omega}{2}(k_{t}-k_{t-1})^2 +(1-\delta) k_{t-1} + (1+r^{\star}+{\color{red}\pi(a_{t-1})})a_{t-1}\] \[y_t = f(k_{t-1}, n_t, z_t)\]

\[z_{t+1} = \rho z_t + \epsilon_{t+1}\]

and \[u(c, n) = \frac{1}{1-\sigma}\left(c^{\psi}(1-n)^{1-\psi} )\right)^{1-\sigma}\]

. . .

The term \(\color{red}\pi\) is there to make the model stationary.

How to make the distribution stationary?

The solution of the model exhibits a unit root:

\[a_t = a_{t-1} + ... \text{other variables in t-1} + \text{shocks in t}\]

. . .

Problem:

there isn’t a unique deterministic steady-state
the ergodic distribution of the model variables is not defined

This raises practical issues (notably for estimation) for the linear model.

no unconditional moments

How to get rid of the unit root?

General idea:

introduce a force that pulls the level of foreign assets towards equilibrium

Schmitt Grohe and Uribe (2003) consider many options:

debt-elastic interest rate: \[1+r = 1+r^{\star} + \pi(a_d)\]
- with \(\pi(0)=0\) and \(\pi^{\prime}(0)>0\)
- \(\pi\) can be understood as a risk premium on rising debt

endogenous time-discount (aka Usawa preferences) \[\beta(c_t) = (1+c_t)^{-\chi}\]
costs of adjustment for international portfolios

. . .

SGU show that the choice of the stationarization device has little effect for the dynamics (moments) of most variables

Calibration

Parameters	Values
\(σ\)	2
\(ψ\)	1.45
\(α\)	0.32
\(ω\)	0.028
\(r\)	0.04

Parameters	Values
\(δ\)	0.1
\(ρ\)	0.42
\(σ²\)	0.0129
\(A^{\star}\)	-0.7442
\(χ\)	0.000742

Results

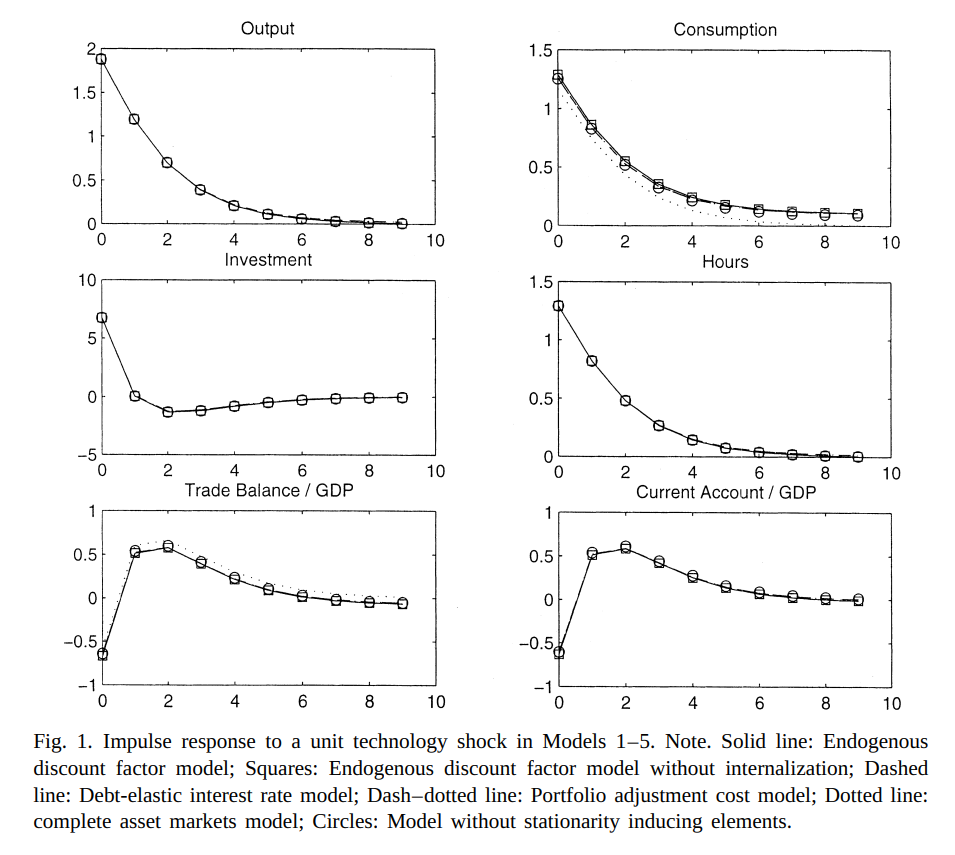
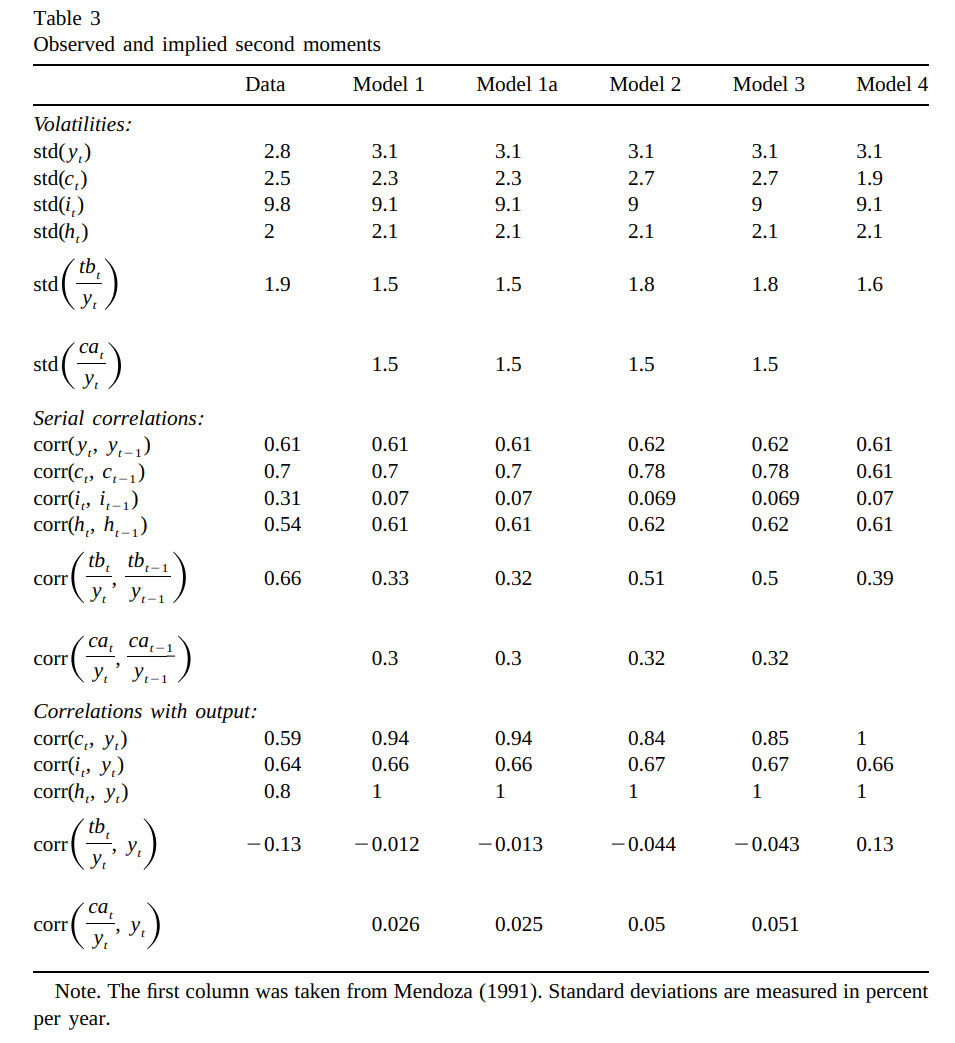
Conclusions

The model matches unconditional correlations fairly well
- The stationarization device has little effect on the moments
Unconditional correlations are not that great
- a limitation of the moment matching method?
Correlation of consumption with output is too high
- and probably cross-correlation of consumption too low
- still the Backus-Kehoe-Kydland puzzle…

Footnotes

Note that initial condition is compatible with the dynare conventions we use here.↩︎