Instrumental variables

IV example on mock dataset

Constructing the dataset

Create four random series of length \(N=1000\)

  • \(x\): education
  • \(y\): salary
  • \(z\): ambition
  • \(q\): early smoking

such that:

  1. \(x\) and \(z\) cause \(y\)
  2. \(z\) causes \(x\)
  3. \(q\) is correlated with \(x\), not with \(z\)

A problem arises when the confounding factor \(z\) is not observed. In that case, we can estimate the direct effect of \(x\) on \(y\) by using \(q\) as an instrument.

Run the follwing code to create a mock dataset.

import numpy as np
import pandas as pd
N = 100000
ϵ_z = np.random.randn(N)*0.1
ϵ_x = np.random.randn(N)*0.1
ϵ_q = np.random.randn(N)*0.01
ϵ_y = np.random.randn(N)*0.01
z = 0.1 + ϵ_z
q = 0.5 + 0.1234*ϵ_x + ϵ_q
# here we must change the definition so that q affects x:
# x = 0.1 + z + ϵ_x
x = 0.1 + z + q + ϵ_x
y  = 1.0 + 0.9*x + 0.4*z + ϵ_y
df = pd.DataFrame({
    "x": x,
    "y": y,
    "z": z,
    "q": q
})

Describe the dataframe. Compute the correlations between the variables. Are they compatible with the hypotheses for IV?

Here are the results from the database:

df.describe()
x y z q
count 100000.000000 100000.000000 100000.000000 100000.000000
mean 0.700385 1.670457 0.100148 0.500003
std 0.150426 0.165036 0.099989 0.015830
min 0.094732 1.001409 -0.365794 0.432416
25% 0.598821 1.559262 0.032510 0.489311
50% 0.700130 1.669901 0.100245 0.499985
75% 0.801383 1.781243 0.167538 0.510676
max 1.308864 2.358062 0.553339 0.571994 
df.corr()
x y z q
x 1.000000 0.981609 0.664405 0.617227
y 0.981609 1.000000 0.787542 0.505723
z 0.664405 0.787542 1.000000 -0.003407
q 0.617227 0.505723 -0.003407 1.000000

We observe: - cor(q, x) non zero: the instrument is relevant - close to zero: might be a weak instrument (we would need to check significance) - cor(q, z) = 0 : the instrument is really exogenous

OLS Regression

Use linearmodels to run a regression estimating the effect of \(x\) on \(y\) (note the slight API change w.r.t. statsmodels). Comment.

What is the problem with this regression? How can it be detected?

from linearmodels import OLS

model = OLS.from_formula("y ~ x", df)
res = model.fit()
res.summary
OLS Estimation Summary
Dep. Variable: y R-squared: 0.9636
Estimator: OLS Adj. R-squared: 0.9636
No. Observations: 100000 F-statistic: 2.64e+06
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:10:57 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
Intercept 0.9162 0.0005 1928.2 0.0000 0.9153 0.9171
x 1.0769 0.0007 1624.8 0.0000 1.0756 1.0782

Regression is globally significant (p-value for Fisher test < 0.00001). The coefficient \(\beta=1.0999\) in front of \(x\) is also very significant at a 0.001% level but does not match the true model for \(y\) (y = 1.0 + 0.9*x + 0.4*z + ϵ_y).

Regress again \(y\) on \(x\), this time controling for missing variable \(z\).

from linearmodels import IV2SLS
formula = (
    "y ~ x + z"
)
mod = IV2SLS.from_formula(formula, df)
res = mod.fit()
res
OLS Estimation Summary
Dep. Variable: y R-squared: 0.9964
Estimator: OLS Adj. R-squared: 0.9964
No. Observations: 100000 F-statistic: 2.729e+07
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:10:59 Distribution: chi2(2)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
Intercept 0.9998 0.0002 5755.9 0.0000 0.9995 1.0002
x 0.9003 0.0003 3219.2 0.0000 0.8998 0.9008
z 0.4000 0.0004 949.12 0.0000 0.3991 0.4008

id: 0x7f4a249d7ef0

Now we see that the coefficient in front of x is the correct one (that is 0.9).

Instrumental variable

Now we try to run a regression without knowing the value of z.

Make a causality graph, summarizing what you know from the equations.

The information about the model’s information structure can be summarized as:

graph TD; X–>Y; Z–>X; Z–>Y; Q–>X;

Use \(q\) to instrument the effect of x on y. Comment.

from linearmodels.iv import IV2SLS

formula = "y ~ 1 + [x ~ q]"
model = IV2SLS.from_formula(formula, df)
result = model.fit()
result
IV-2SLS Estimation Summary
Dep. Variable: y R-squared: 0.9372
Estimator: IV-2SLS Adj. R-squared: 0.9372
No. Observations: 100000 F-statistic: 4.067e+05
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:16:05 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
Intercept 1.0409 0.0010 1046.4 0.0000 1.0389 1.0428
x 0.8989 0.0014 637.73 0.0000 0.8962 0.9017


Endogenous: x
Instruments: q
Robust Covariance (Heteroskedastic)
Debiased: False
id: 0x7f4a249d63c0

We observe that the result is, again, the correct one. This is especially impressive since we didn’t have access to the confounding factor z and couldn’t add it to the regression. Instead, we had another source of randomness q that we used to instrument the regression.

Return on Education

We follow the excellent R tutorial from the (excellent) Econometrics with R book.

The goal is to measure the effect of schooling on earnings, while correcting the endogeneity bias by using distance to college as an instrument.

Download the college distance using get_dataset function and make a nice dataframe. Describe the dataset. Plot a histogram of distance (you can use matplotlib’s hist function or seaborn).

https://vincentarelbundock.github.io/Rdatasets/datasets.html

import statsmodels.api as sm
ds = sm.datasets.get_rdataset("CollegeDistance", "AER")
# the dataframe must be retrieved from the dataset object
df = ds.data
df.head()
gender ethnicity score fcollege mcollege home urban unemp wage distance tuition education income region
rownames
1 male other 39.150002 yes no yes yes 6.2 8.09 0.2 0.88915 12 high other
2 female other 48.869999 no no yes yes 6.2 8.09 0.2 0.88915 12 low other
3 male other 48.740002 no no yes yes 6.2 8.09 0.2 0.88915 12 low other
4 male afam 40.400002 no no yes yes 6.2 8.09 0.2 0.88915 12 low other
5 female other 40.480000 no no no yes 5.6 8.09 0.4 0.88915 13 low other 
df.describe()
score unemp wage distance tuition education
count 4739.000000 4739.000000 4739.000000 4739.000000 4739.000000 4739.000000
mean 50.889029 7.597215 9.500506 1.802870 0.814608 13.807765
std 8.701910 2.763581 1.343067 2.297128 0.339504 1.789107
min 28.950001 1.400000 6.590000 0.000000 0.257510 12.000000
25% 43.924999 5.900000 8.850000 0.400000 0.484990 12.000000
50% 51.189999 7.100000 9.680000 1.000000 0.824480 13.000000
75% 57.769999 8.900000 10.150000 2.500000 1.127020 16.000000
max 72.809998 24.900000 12.960000 20.000000 1.404160 18.000000

How is education encoded? Create a binary variable education_binary to replace it.

df['income'].unique()
# education variable takes string values ("high" or "low"). 
array(['high', 'low'], dtype=object)
# we need to convert them into 1 and 0 first
df['income_binary'] = (df['income'] == "high")*1
# other option 1
df['incomeb'] = df['income'].map({'high' : 1, 'low': 0})
# other option 2
df['incomeb'] = (df['income'] == 'high')*1

Plot an histogram of distance to college.

from matplotlib import pyplot as plt
plt.hist(df['distance'])
(array([3241.,  831.,  399.,  156.,   45.,   17.,   10.,   19.,   17.,
           4.]),
 array([ 0.,  2.,  4.,  6.,  8., 10., 12., 14., 16., 18., 20.]),
 <BarContainer object of 10 artists>)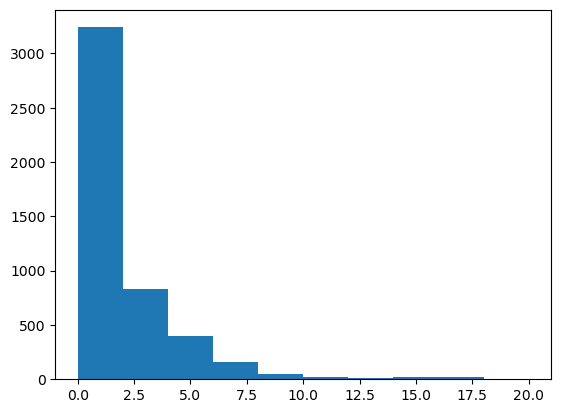

# same with seaborn
import seaborn as sns
sns.histplot(df['distance'])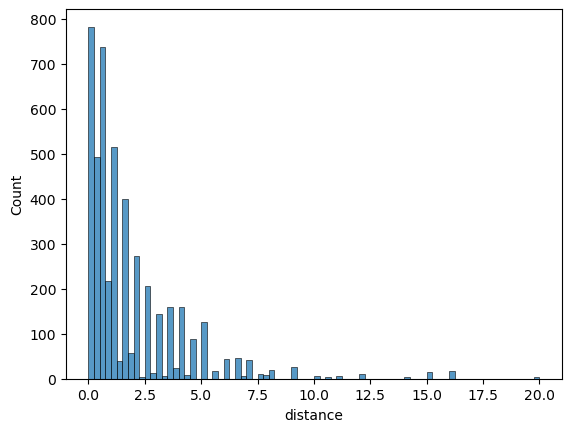

Run the naive regression \(\text{incomeb}=\beta_0 + \beta_1 \text{education} + u\) using linearmodels. Comment.

from linearmodels.iv import IV2SLS # we can use IV2SLS instead of OLS to run regular regressions

formula = "incomeb ~ education"
model = IV2SLS.from_formula(formula, df)
result = model.fit()
result
OLS Estimation Summary
Dep. Variable: incomeb R-squared: 0.0480
Estimator: OLS Adj. R-squared: 0.0478
No. Observations: 4739 F-statistic: 227.43
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:17:44 Distribution: chi2(1)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
Intercept -0.4780 0.0499 -9.5702 0.0000 -0.5759 -0.3801
education 0.0555 0.0037 15.081 0.0000 0.0483 0.0627

id: 0x7f4a182e7da0

We find that education explains higher income with a significant, but low coefficient 0.05.

Augment the regression with unemp, hispanic, af-am, female and urban. Notice that categorical variables are encoded automatically. What are the treatment values? Change it using the syntax (C(var,Treatment='ref'))

from linearmodels.iv import IV2SLS

formula = "incomeb ~ education + unemp + gender + ethnicity"
model = IV2SLS.from_formula(formula, df)
result = model.fit()
result
OLS Estimation Summary
Dep. Variable: incomeb R-squared: 0.0811
Estimator: OLS Adj. R-squared: 0.0802
No. Observations: 4739 F-statistic: 443.38
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:17:47 Distribution: chi2(5)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
Intercept -0.4361 0.0533 -8.1797 0.0000 -0.5406 -0.3316
education 0.0511 0.0037 13.982 0.0000 0.0439 0.0582
unemp -0.0111 0.0022 -4.9609 0.0000 -0.0155 -0.0067
gender[T.male] 0.0484 0.0128 3.7866 0.0002 0.0234 0.0735
ethnicity[T.hispanic] -0.0249 0.0185 -1.3425 0.1794 -0.0612 0.0114
ethnicity[T.other] 0.1347 0.0163 8.2871 0.0000 0.1029 0.1666

id: 0x7f4a18106ff0 
df['ethnicity'].unique()
array(['other', 'afam', 'hispanic'], dtype=object)

In the regression above, some variables have been created for each value of the categorical vairables (save for the reference value which doesn’t appear). In the case of variable ethnicity, we see that hispanic and other are two of the three values taken by variable ethnicity. This means that value afam was taken as reference.

We can change the reference variable as follows:

# needed only if you use the function Treatment in the formulas
from linearmodels.iv import IV2SLS

formula = "incomeb ~ education + unemp + C(gender) + C(ethnicity,Treatment(reference='other'))"
model = IV2SLS.from_formula(formula, df)
result = model.fit()
result
OLS Estimation Summary
Dep. Variable: incomeb R-squared: 0.0811
Estimator: OLS Adj. R-squared: 0.0802
No. Observations: 4739 F-statistic: 443.38
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:17:51 Distribution: chi2(5)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
Intercept -0.3014 0.0540 -5.5788 0.0000 -0.4073 -0.1955
education 0.0511 0.0037 13.982 0.0000 0.0439 0.0582
unemp -0.0111 0.0022 -4.9609 0.0000 -0.0155 -0.0067
C(gender)[T.male] 0.0484 0.0128 3.7866 0.0002 0.0234 0.0735
C(ethnicity, Treatment(reference='other'))[T.afam] -0.1347 0.0163 -8.2871 0.0000 -0.1666 -0.1029
C(ethnicity, Treatment(reference='other'))[T.hispanic] -0.1596 0.0149 -10.710 0.0000 -0.1888 -0.1304

id: 0x7f4a181d6630

Comment the results and explain the endogeneity problem

Adding additional regressors has increased the fit (adj. R^2 from 0.04 to 0.08) without changing the coefficient on the education level. This would imply that regression is robust.

However, we might have an endogeneity issue with some potential other factors explaining both income level and salary (cf many discussions in the course).

Explain why distance to college might be used to instrument the effect of schooling.

Assuming that the decision to live in a given county does not depend on the presence of a college nearby, the distance to college should be exogenous.

The distance to college is probably correlated with the decision to go so the instrument should have some power (opposite of weak)

Run an IV regression, where distance is used to instrument schooling.

look at: https://bashtage.github.io/linearmodels/ (two-stage least squares)

from linearmodels.iv import IV2SLS
 
formula = "incomeb ~ [education ~ distance] + unemp + C(gender) + C(ethnicity, Treatment(reference='other'))"
model = IV2SLS.from_formula(formula, df)
result = model.fit()
result
IV-2SLS Estimation Summary
Dep. Variable: incomeb R-squared: -0.1339
Estimator: IV-2SLS Adj. R-squared: -0.1351
No. Observations: 4739 F-statistic: 1748.5
Date: Wed, Feb 21 2024 P-value (F-stat) 0.0000
Time: 15:18:14 Distribution: chi2(6)
Cov. Estimator: robust
Parameter Estimates
Parameter Std. Err. T-stat P-value Lower CI Upper CI
unemp -0.0100 0.0025 -3.9704 0.0001 -0.0149 -0.0051
C(gender)[T.female] -1.9566 0.5039 -3.8830 0.0001 -2.9441 -0.9690
C(gender)[T.male] -1.9109 0.5042 -3.7897 0.0002 -2.8991 -0.9226
C(ethnicity, Treatment(reference='other'))[T.afam] -0.0753 0.0259 -2.9005 0.0037 -0.1261 -0.0244
C(ethnicity, Treatment(reference='other'))[T.hispanic] -0.1247 0.0203 -6.1432 0.0000 -0.1645 -0.0849
education 0.1692 0.0358 4.7261 0.0000 0.0990 0.2393


Endogenous: education
Instruments: distance
Robust Covariance (Heteroskedastic)
Debiased: False
id: 0x7f4a17f31190

Comment the results.

The estimate we get for the return on education is three times higher than without the instrument and highly significant.