Introduction to Machine Learning (2)

Data-Based Economics, ESCP, 2024-2025

Author

Pablo Winant

Published

March 4, 2025

Classification Problems

Classification problem

  • Binary Classification
    • Goal is to make a prediction \(c_n = f(x_{1,1}, ... x_{k,n})\) …
    • …where \(c_i\) is a binary variable (\(\in\{0,1\}\))
    • … and \((x_{i,n})_{k\in[1,n]}\), \(k\) different features to predict \(c_n\)
  • Multicategory Classification
    • The variable to predict takes values in a non ordered set with \(p\) different values

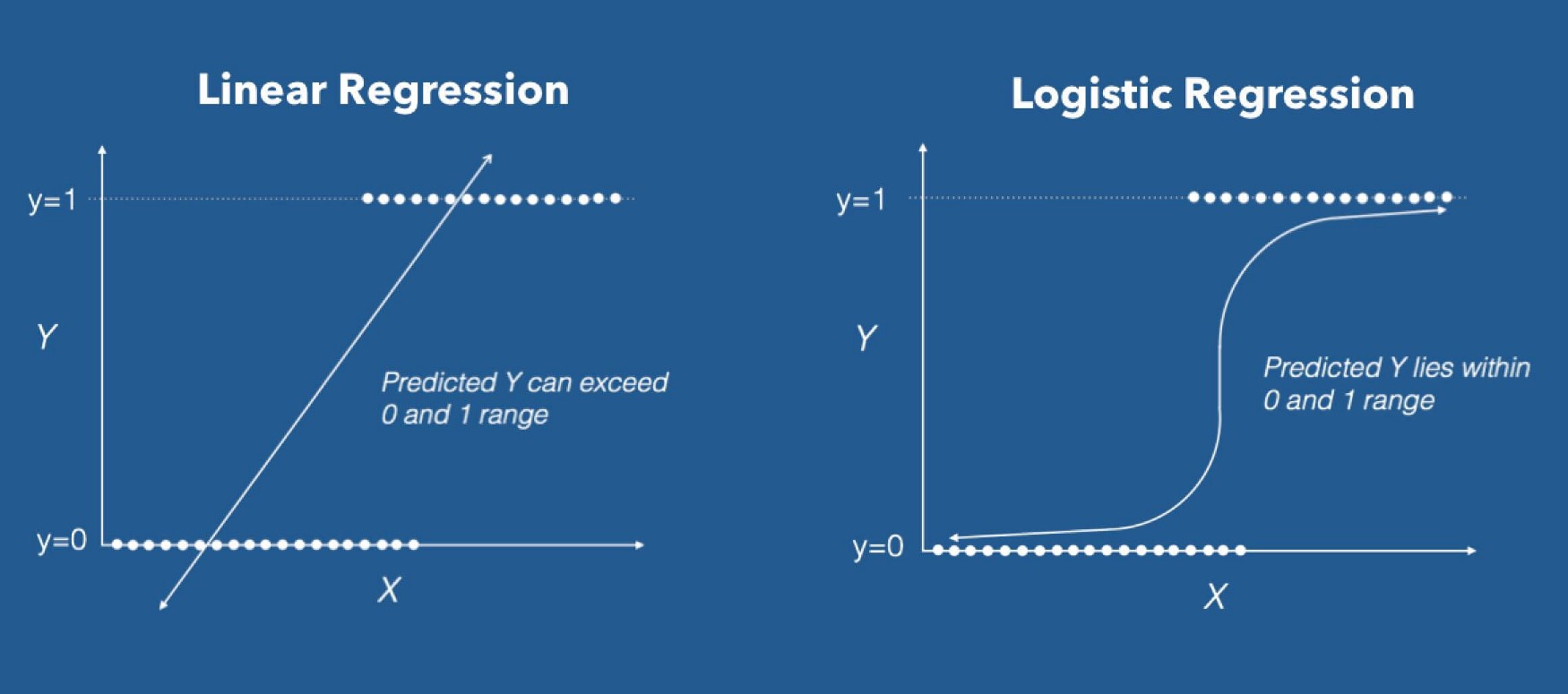
Logistic regression

  • Given a regression model (a linear predictor) \[ a_0 + a_1 x_1 + a_2 x_2 + \cdots a_n x_n \]
  • one can build a classification model: \[ f(x_1, ..., x_n) = \sigma( a_0 + a_1 x_1 + a_2 x_2 + \cdots a_n x_n )\] where \(\sigma(x)=\frac{1}{1+\exp(-x)}\) is the logistic function a.k.a. sigmoid
  • The loss function to minimize is: \[L() = \sum_n (c_n - \sigma( a_{0} + a_1 x_{1,n} + a_2 x_{2,n} + \cdots a_k x_{k,n} ) )^2\]
  • This works for any regression model (LASSO, RIDGE, nonlinear…)

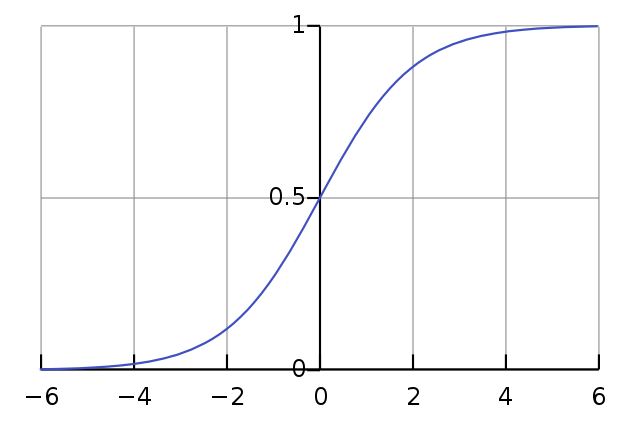
Logistic regression

  • The linear model predicts an intensity/score (not a category) \[ f(x_1, ..., x_n) = \sigma( \underbrace{a_0 + a_1 x_1 + a_2 x_2 + \cdots a_n x_n }_{\text{score}})\]
  • \(f\) can be interpreted as the “probability” to be 1 rather than 0.
  • To make a prediction: round to 0 or 1.

Multinomial regression

  • If there are \(P\) categories to predict:
    • build a linear predictor \(f_p\) for each category \(p\)
    • linear predictor is also called score
  • To predict:
    • evaluate the score of all categories
    • choose the one with highest score
  • To train the model:
    • train separately all scores (works for any predictor, not just linear)
    • … there are more subtle approaches (not here)

Other Classifiers

Common classification algorithms

There are many:

  • Logistic Regression
  • Naive Bayes Classifier
  • Nearest Distance
  • neural networks (replace score in sigmoid by n.n.)
  • Decision Trees
  • Support Vector Machines

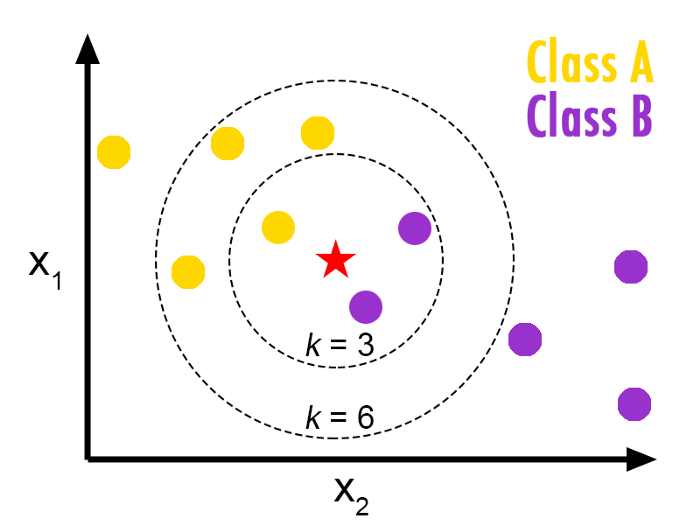
Nearest distance

  • Idea:
    • in order to predict category \(c\) corresponding to \(x\) find the closest point \(x_0\) in the training set
    • Assign to \(x\) the same category as \(x_0\)
  • But this would be very susceptible to noise
  • Amended idea: \(k-nearest\) neighbours
    • look for the \(k\) points closest to \(x\)
    • label \(x\) with the same category as the majority of them
  • Remark: this algorithm uses Euclidean distance. This is why it is important to normalize the dataset.

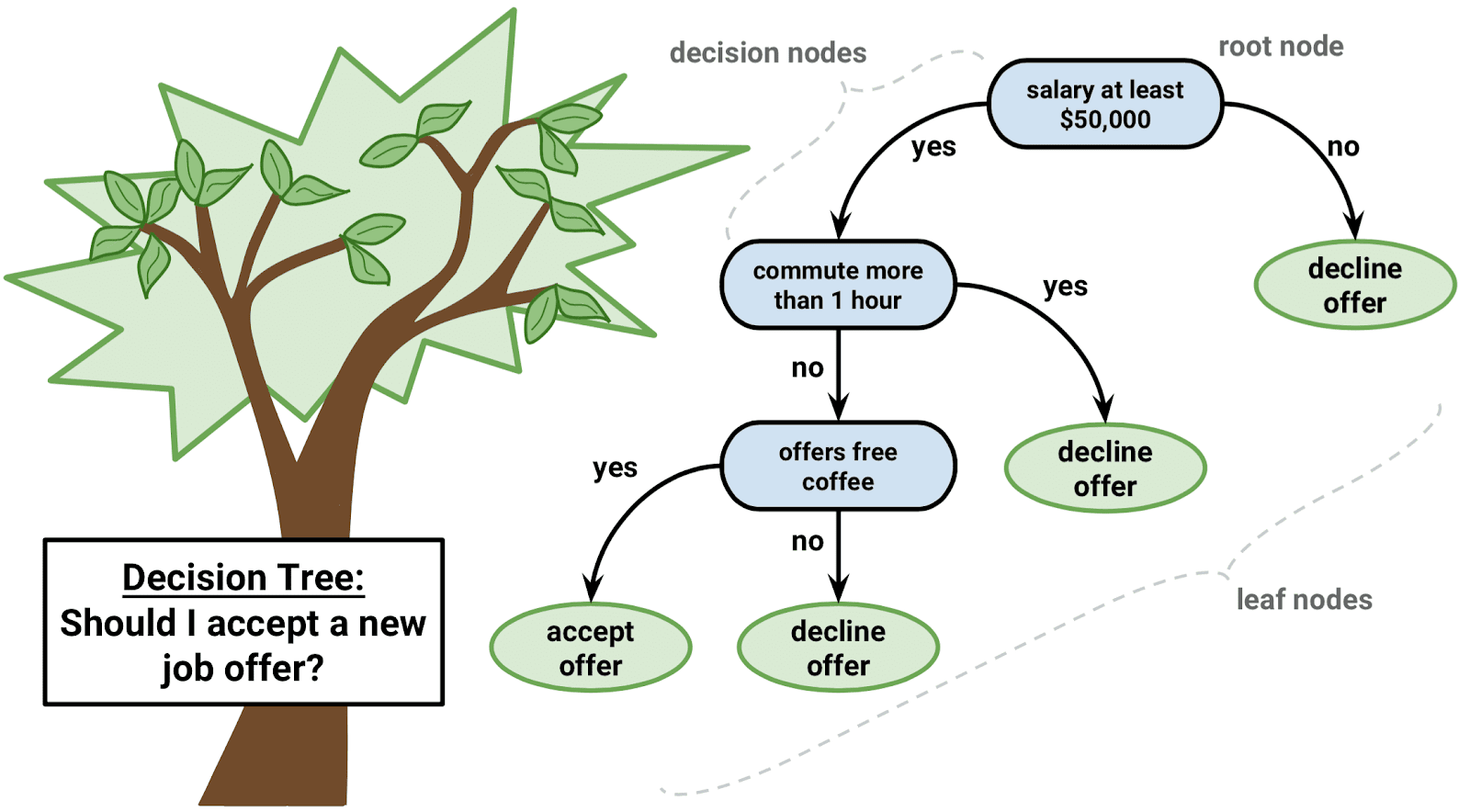
Decision Tree / Random Forests

  • Decision Tree
    • recursively find simple criteria to subdivide dataset
  • Problems:
    • Greedy: algorithm does not simplify branches
    • easily overfits
  • Extension : random tree forest
    • uses several (randomly generated) trees to generate a prediction
    • solves the overfitting problem

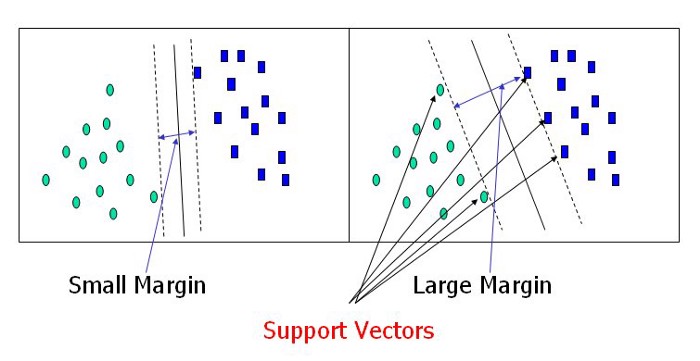
Support Vector Classification

  • Separates data by one line (hyperplane).
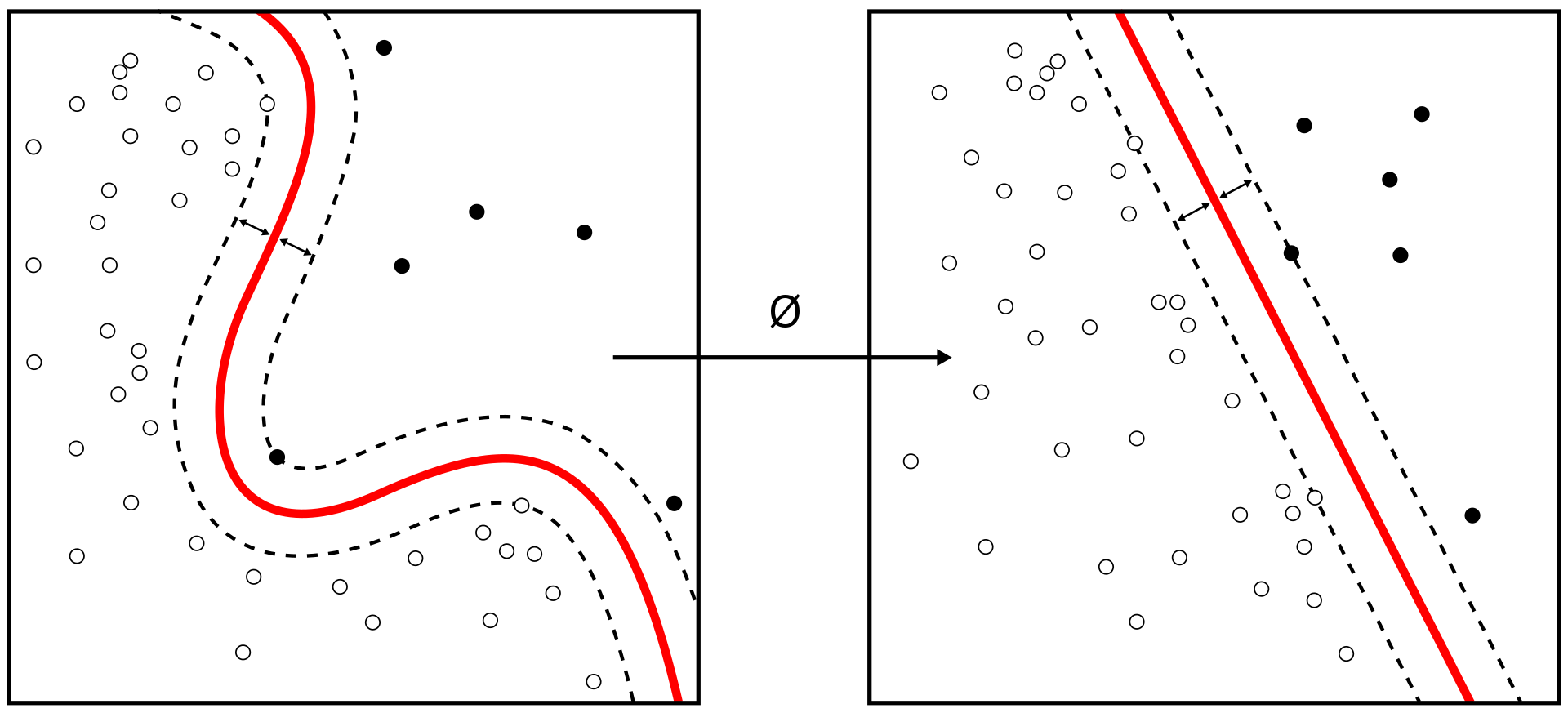
  • Chooses the largest margin according to support vectors
  • Can use a nonlinear kernel.

All these algorithms are super easy to use!

Examples:

  • Decision Tree
from sklearn.tree import DecisionTreeClassifier
clf = DecisionTreeClassifier(random_state=0)

. . .

  • Support Vector
from sklearn.svm import SVC
clf = SVC(random_state=0)

. . .

  • Ridge Regression
from sklearn.linear_model import Ridge
clf = Ridge(random_state=0)

Validation

Validity of a classification algorithm

  • Independently of how the classification is made, its validity can be assessed with a similar procedure as in the regression.

  • Separate training set and test set

    • do not touch test set at all during the training

  • Compute score: number of correctly identified categories

    • note that this is not the same as the loss function minimized by the training

Classification matrix

  • For binary classification, we focus on the classification matrix or confusion matrix.
Predicted (0) Actual (1) Actual
0 true negatives (TN) false negatives (FN)
1 false positives (FP) true positives (TP)

. . .

We can then define different measures:

  • Sensitivity aka True Positive Rate (TPR): \(\frac{TP}{FP+TP}\)
  • False Positive Rate (FPR): \(\frac{FP}{TN+FP}\)
  • Overall accuracy: \(\frac{\text{TN}+\text{TP}}{\text{total}}\)

. . .

Which one to favour depends on the use case

Example: London Police

Police cameras in London

According to London Police the cameras in London have

  • True Positive Identification rate of over 80% at a fixed number of False Positive Alerts.29 nov. 2022

. . .

But reporters found a 81% are misidentication rate

. . .

Interpretation? Is it working?

Example

In-sample confusion matrix

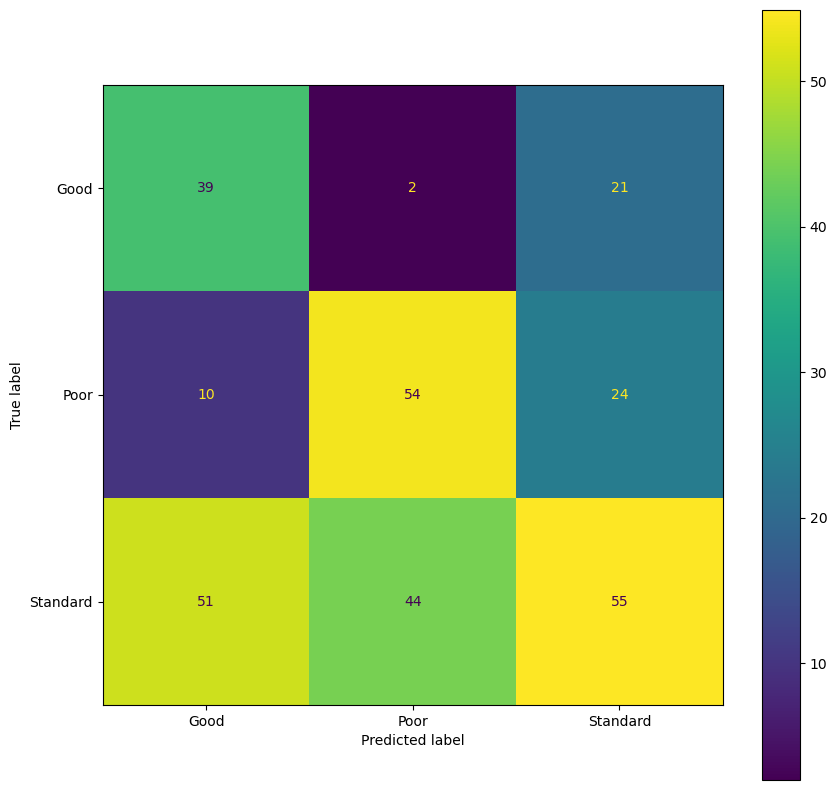
Based on consumer data, an algorithm tries to predict the credit score from various client characeristics. The predictions are reported in the confusion matrix.

Can you calculate: FPR, TPR and overall accuracy?

Confusion matrix with sklearn

  • Predict on the test set:
y_pred = model.predict(x_test)
  • Compute confusion matrix:
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)