Introduction to Instrumental Variables

Data-Based Economics, ESCP, 2024-2025

Pablo Winant

2025-02-12

Categorical Variables

Data

Our multilinear regression: \[y = \alpha + \beta x_1 + \cdots + \beta x_n\]

So far, we have only considered real variables: (\(x_i \in \mathbb{R}\)).

Like: \[x_{\text{gdp}} = \alpha + \beta_1 x_{\text{unemployment}} + \beta_2 x_{\text{inflation}}\]

Data

How do we deal with the following cases?

binary variable: \(x\in \{0,1\}\) (or \(\{True, False\}\))
- ex: \(\text{gonetowar}\), \(\text{hasdegree}\)
categorical variable:
- ex: survey result (0: I don’t know, 1: I strongly disagree, 2: I disagree, 3: I agree, 4: I strongly agree)
- there is no ranking of answers
- when there is ranking: hierarchical index
nonnumerical variables:
- ex: (flower type: \(x\in \text{myosotis}, \text{rose}, ...\))

Binary variable

Nothing to be done: just make sure variables take values 0 or 1. \[y_\text{salary} = \alpha + \beta x_{\text{gonetowar}}\]
Interpretation:
- having gone to war is associated with a \(\beta\) increase (or decrease?) in salary (still no causality)

Categorical variable

Look at the model: \[y_{\text{CO2 emission}} = \alpha + \beta x_{\text{banish cars}} \]

where \(y_{\text{CO2 emission}}\) is an individual’s CO2 emissions and \(x_{\text{yellow vest support}}\) is the response the the question Do you suport the banishment of petrol cars?.

Response is coded up as:

0: Strongly disagree
1: Disagree
2: Neutral
3: Agree
4: Strongly agree

If the variable was used directly, how would you intepret the coefficient \(\beta\) ?

index is hierarchical
but the distances between 1 and 2 or 2 and 3 are not comparable…

Hierarchical index

We use one dummy variable per possible answer.

\(D_{\text{Strongly Disagree}}\)	\(D_{\text{Disagree}}\)	\(D_{\text{Agree}}\)	\(D_{\text{Strongly Agree}}\)
1	0	0	0
0	1	0	0
0	0	0	0
0	0	1	0
0	0	0	1

Hierarchical index

Values are linked by the specific dummy coding.
- the choice of the reference group (with 0) is not completely neutral
  - for linear regressions, we can ignore its implications
- it must be frequent enough in the data
Note that hierarchy is lost. The same treatment can be applied to non-hierachical variables
Now our variables are perfectly colinear:
- we can deduce one from all the others
- we drop one from the regression: the reference group TODO

Hierarchical index (2)

\[y_{\text{CO2 emission}} = \alpha + \beta_1 x_{\text{strdis}} + \beta_2 x_{\text{dis}} + \beta_3 x_{\text{agr}} + \beta_4 x_{\text{stragr}}\]

Interpretation:
- being in the group which strongly agrees to the yellow vest’s claim is associated with an additional \(\beta_4\) increase in CO2 consumption compared with members of the neutral group

Nonnumerical variables

What about nonnumerical variables?
When variables take nonnumerical variables, we convert them to numerical variables.
Example:

activity	code
massage therapist	1
mortician	2
archeologist	3
financial clerks	4

Then we convert to dummy variables exactly like hierarchical indices
- here \(\text{massage therapist}\) is taken as reference

\(D_{\text{mortician}}\)	\(D_{\text{archeologist}}\)	\(D_{\text{financial clerks}}\)
1	0	0
0	1	0
0	0	1

Hands-on

Use statsmodels/linearmodels to create dummy variables with formula API.

Replace

salary ~ activity

salary ~ C(activity)

There is an options to choose the reference group

salary ~ C(activity, Treatment(reference="archeologist"))

Causality

What is causality?

Clear? Huh! Why a four-year-old child could understand this report! Run out and find me a four-year-old child, I can’t make head or tail of it.

Spurious correlation

Spurious Correlation

We have seen spurious correlation before
- it happens when two series comove without being actually correlated
Also, two series might be correlated without one causing the other
- ex: countries eating more chocolate have more nobel prices…

Definitions?

But how do we define

correlation
causality

Both concepts are actually hard to define:

in statistics (and econometrices) they refer to the generating process
if the data was generated again, would you observe the same relations?

For instance correlation between \(X\) and \(Y\) is just the average correlation taken over many draws \(\omega\) of the data: \[E_{\omega}\left[ (X-E[X])(Y-E[Y])\right]\]

How do we define causality (1)

In math, we have implication: \(A \implies B\)
- applies to statements that can be either true or false
- given \(A\) and \(B\), \(A\) implies \(B\) unless \(A\) is true and \(B\) is false
- paradox of the drinker: at any time, there exists a person such that: if this person drinks, then everybody drinks
In a mathematical universe taking values \(\omega\), we can define causality between statement \(A(\omega)\) and \(B(\omega)\) as : \[\forall \omega, A(\omega) \implies B(\omega)\]

How do we define causality (2)

But causality in the real world is problematic

Usually, we observe \(A(\omega)\) only once…

Example:

state of the world \(\omega\): 2008, big financial crisis, …
A: Ben Bernanke chairman of the Fed
B: successful economic interventions
Was Ben Bernanke a good central banker?
Impossible to say.

Causality in Statistics

Statistical definition of causality

Variable \(A\) causes \(B\) in a statistical sense if

\(A\) and \(B\) are correlated
\(A\) is known before \(B\)
correlation between \(A\) and \(B\) is unaffected by other variables

There are other related statistical definitions:
- like Granger causality…
- … but not for this course

Experiments

Factual and counterfactual

Suppose we observe an event A
- A: a patient is administered a drug, government closes all schools during Covid
We observe a another event B
- B: the patient recovers, virus circulation decreases

To interpret B as a consequence of A, we would like to consider the counter-factual:
- a patient is not administered a drug, government doesn’t close schools
- patient does not recover, virus circulation is stable

An important task in econometrics is to construct a counter-factual

as the name suggests is it sometimes never observed!

Scientific Experiment

In science we establish causality by performing experiments
- and create the counterfactual
A good experiment is reproducible
- same variables
- same state of the world (other variables)
- reproduce several times (in case output is noisy or random)
Change one factor at a time
- to create a counter-factual

Measuring effect of treatment

Assume we have discovered two medications: R and B

Give one of them (R) to a patient and observe the outcome

Would would have been the effect of (B) on the same patient?
- ????

What if we had many patients and let them choose the medication?

Maybe the effect would be the consequence of the choice of patients rather than of the medication?

An exmple from behavioural economics

Example: cognitive dissonance

Experiment in GATE Lab (ENS Lyon)
Volunteers play an investment game.
They are asked beforehand whether they support OM, PSG, or none.

Experiment 1:
- Before the experiment, randomly selected volunteers are given a football shirt of their preferred team (treatment 1)
- Other volunteers receive nothing (treatment 0)
Result:
- having a football shirt seems to boost investment performance…

Experiment 2: subjects are given randomly a shirt of either Olympique de Marseille or PSG.
Result:
- Having the good shirt improves performance.
- Having the wrong one deteriorates it badly.

How would you code up this experiment?
Can we conclude on some form of causality?

Formalisation of the problem

Cause (A): two groups of people
- those given a shirt (treatment 1)
- those not given a shirt (treatment 0)
Possible consequence (B): performance
Take a given agent Alice: she performs well with a PSG shirt.
- maybe she is a good investor?
- or maybe she is playing for her team?
Let’s try to have her play again without the football shirt
- now the experiment has changed: she has gained experience, is more tired, misses the shirt…
- it is impossible to get a perfect counterfactual (i.e. where only A changes)

Let’s take somebody else then? Bob was really bad without a PSG shirt.
- he might be a bad investor? or he didn’t understand the rules?
- some other variables have changed, not only the treatment
How to make a perfect experiment?
- Choose randomly whether assigning a shirt or not
- by construction the treatment will not be correlated with other variables

Randomized Control Trial

Randomized Control Trial (RCT)

The best way to ensure that treatment is independent from other factors is to randomize it.

In medecine

some patients receive the treatment (red pill)
some other receive the control treatment (blue pill / placebo)

In economics:

randomized field experiments
randomized phase-ins for new policies
- very useful for policy evaluation

Natural experiment

Natural Experiment

A natural experiment satisfies conditions that treatment is assigned randomly

without interference by the econometrician

An exemple of a Natural Experiment:

gender bias in french local elections (jean-pierre eymeoud, paul vertier) link
are women discriminated against by voters in local elections?

Result: yes, they get 1.5% less votes by right-wing voters

What was the natural experiment?

Instrumental variables

Example

Lifetime Earnings and the Vietnam Era Draft Lottery, by JD Angrist

Fact:

veterans of the vietnam war (55-75) earn (in the 80s) an income that is 15% less in average than those who didn’t go to the war.
What can we conclude?
Hard to say: maybe those sent to the war came back with lower productivity (because of PTSD, public stigma, …)? maybe they were not the most productive in the first place (unobserved selection bias)?

Problem (for the economist):

we didn’t send people to war randomly

Genius idea:

here is a variable which randomly affected whether people were sent: the Draft
between 1947, and 1973, a lottery was run to determine who would go to war
the draft number was determined, based on date of birth, and first letters of name
and was correlated with the probability that a given person would go to war
and it was so to say random or at least independent from anything relevant to the problem

Can we use the Draft to generate randomness ?

Problem

Take the linear regression: \[y = \alpha + \beta x + \epsilon\]
- \(y\): salary
- \(x\): went to war
We want to establish causality from x to y
- we would like to interpret \(x\) as the “treatment”
But there can be unobserved confounding factors:
- variable \(z\) which causes both x and y
- exemple: socio-economic background, IQ, …
If we could identify \(z\) we could control for it: \[y = \alpha + \beta_1 x + \beta_2 z + \epsilon\]
- we would get a better predictor of \(y\) but more uncertainty about \(\beta_1\) (\(x\) and \(z\) are correlated)

Reformulate the problem

Let’s assume treatment \(x\) is a binary variable \(\in{0,1}\)
We want to estimate \[y = \alpha + \beta x + z + \epsilon\] where \(z\) is potentially correlated to \(x\) and \(y\)
There are two groups:
- those who receive the treatment \[y = \alpha + \beta + z_{T=1} + \epsilon\]
- the others \[y = \alpha + 0 + z_{T=0} + \epsilon\]

Problem:
- if \(z\) is higher in the treatment group, its effect can’t be separated from the treatment effect.
Intuition: what if we make groups differently?
- completely independent from \(z\) (and \(\epsilon\))
- not independently from \(x\) so that one group will receive more treatment than the other
To make this group we need a new variable \(q\) that is:
- correlated with \(x\) so that it will correspond to some treatment effect
- uncorrelated to \(z\) or \(\epsilon\) (exogenous)

Two stage regression

We would like to redo the treatment groups in a way that is independent from \(z\) (and everything contained in \(\epsilon\))
- \(q\) is a binary variable: drafted or not
First stage: regress group assignment on the instrument: \[x = \alpha_0 + \beta_0 q + \eta\]
- we can now predict group assignment in a way that is independent from \(z\) (and everything in \(\epsilon\)) \[\tilde{x} = \alpha_0 + \beta_0 q\]
Second stage: use the predicted value instead of the original one \[y = \alpha + \beta_1 \tilde{x} + z + \epsilon\]

Result:
- If \(\beta_1\) is significantly nonzero, there is a causal effect between \(x\) and \(y\).
- Note that \(\tilde{x}\) is imperfectly correlated with the treatment: \(\beta_1\) can’t be interpreted directly
- The actual effect will be \(\frac{\beta_1}{\beta_0}\) (in 1d)
We say that we instrument \(x\) by \(q\).

Choosing a good instrument

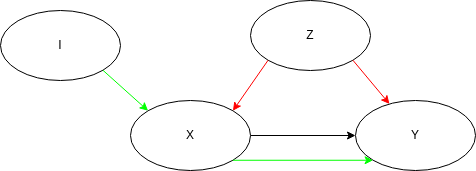
Choosing an instrumental variable

A good instrument when trying to explain y by x, is a variable that is correlated to the treatment (x) but does not have any effect on the outcome of interest (y), appart from its effect through x.

In particular, it should be uncorrelated from any potential confounding factor (whether observed or unobserved).

In practice

Both statsmodels and linearmodels support instrumental variables
- library (look for IV2SLS)
Library linearmodels has a handy formula syntax: salary ~ 1 + [war ~ draft]
- API is similar but not exactly identical to statsmodels
Example from the doc

formula = (
    "np.log(drugexp) ~ 1 + totchr + age + linc + blhisp + [hi_empunion ~ ssiratio]"
)
ols = IV2SLS.from_formula(formula, data)
ols_res = ols.fit(cov_type="robust")
print(ols_res)