Optimization

Macroeconomics: Numerical Methods

Year 2023-2024 (MIE37)

2024-04-04

Introduction

Introduction

Optimization is everywhere in economics:

  • to model agent’s behaviour: what would a rational agent do?
    • consumer maximizes utility from consumption
    • firm maximizes profit
  • an economist tries to solve a model:
    • find prices that clear the market

Two kinds of optimization problem:

  • root finding: \(\text{find $x$ in $X$ such that $f(x)=0$}\)

  • minimization/maximization \(\min_{x\in X} f(x)\) or \(\max_{x\in X} f(x)\)

  • often a minimization problem can be reformulated as a root-finding problem

    \[x_0 = {argmin}_{x\in X} f(x) \overbrace{\iff}^{??} f^{\prime} (x_0) = 0\]

Plan

  • general consideration about optimization problems
  • one-dimensional root-finding
  • one-dimensional optimization
  • local root-finding
  • local optimization
  • constrained optimization
  • constrained root-finding

General considerationsre

Optimization tasks come in many flavours

  • continuous versus discrete optimization
  • constrained and unconstrained optimization
  • global and local
  • stochastic and deterministic optimization
  • convexity

Continuous versus discrete optimization

  • Choice is picked from a given set (\(x\in X\)) which can be:
    • continuous: choose amount of debt \(b_t \in [0,\overline{b}]\), of capital \(k_t \in R^{+}\)
    • discrete: choose whether to repay or default \(\delta\in{0,1}\), how many machines to buy (\(\in N\)), at which age to retire…
    • a combination of both: mixed integer programming

Continuous versus discrete optimization (2)

  • Discrete optimization requires a lot of combinatorial thinking
    • We don’t cover it today.
    • …if needed, we just test all choices until we find the best one
  • Sometimes a discrete choice can be approximated by a mixed strategy (i.e. a random strategy).
    • Instead of \(\delta\in{0,1}\) we choose \(x\) in \(prob(\delta=1)=\sigma(x)\)
    • with \(\sigma(x)=\frac{2}{1+\exp(-x)}\)

Constrained and Unconstrained optimization

  • Unconstrained optimization: \(x\in R\)
  • Constrained optimization: \(x\in X\)
    • budget set: \(p_1 c_1 + p_2 c_2 \leq I\)
    • positivity of consumption: \(c \geq 0\).
  • In good cases, the optimization set is convex…
    • pretty much always in this course

Stochastic vs Determinstic

  • Common case, especially in machine learning \[f(x) = E_{\epsilon}[ \xi (\epsilon, x)]\]
  • One wants to maximize (resp solve) w.r.t. \(x\) but it is costly to compute expectation precisely using Monte-Carlo draws (there are other methods).
  • A stochastic optimization method allows to use noisy estimates of the expectation, and will still converge in expectation.
  • For now we focus on deterministic methods. Maybe later…

Local vs global Algorithms

  • In principle, there can be many roots (resp maxima) within the optimization set.

  • Algorithms that find them all are called “global”. For instance:

    • grid search
    • simulated annealing

  • We will deal only with local algorithms, and consider local convergence properties.

    • ->then it might work or not
    • to perform global optimization just restart from different points.

Math vs practice

  • The full mathematical treatment will typically assume that \(f\) is smooth (\(\mathcal{C}_1\) or \(\mathcal{C}_2\) depending on the algorithm).

  • In practice we often don’t know about these properties

    • we still try and check thqt we have a local optimal

  • So: fingers crossed

Math vs practice

Here is the surface representing the objective that a deep neural network training algorithm tries to minimize.

And yet, neural networks do great things!

What do you need to know?

  • be able to handcode simple algos (Newton, Gradient Descent)
  • understand the general principle of the various algorithms to compare them in terms of
    • robustness
    • efficiency
    • accuracy
  • then you can just switch the various options, when you use a library…

One-dimensional root-finding

Bisection

  • Find \(x \in [a,b]\) such that \(f(x) = 0\). Assume \(f(a)f(b) <0\).
  • Algorithm
    1. Start with \(a_n, b_n\). Set \(c_n=(a_n+b_n)/2\)
    2. Compute \(f(c_n)\)
    • if \(f(c_n)f(a_n)<0\) then set \((a_{n+1},b_{n+1})=(a_n,c_n)\)
    • else set \((a_{n+1},b_{n+1})=(c_n,b_n)\)
    1. If \(|f(c_n)|<\epsilon\) and/or \(\frac{b-a}{2^n}<\delta\) stop. Otherwise go back to 1.

Bisection (2)

  • No need for initial guess: globally convergent algorithm
    • not a global algorithm…
    • … in the sense that it doesn’t find all solutions
  • \(\delta\) is a guaranteed accuracy on \(x\)
  • \(\epsilon\) is a measure of how good the solution is
  • think about your tradeoff: (\(\delta\) or \(\epsilon\) ?)

Newton algorithm

  • Find \(x\) such that \(f(x) = 0\). Use \(x_0\) as initial guess.
  • \(f\) must be \(\mathcal{C_1}\) and we assume we can compute its derivative \(f^{\prime}\)
  • General idea:
    • observe that the zero \(x^{\star}\) must satisfy \[f(x^{\star})=0=f(x_0)+f^{\prime}(x_0)(x^{\star}-x_0) + o(x-x_0)\]
    • Hence a good approximation should be \[x^{\star}\approx = x_0- f(x_0)/f^{\prime}(x_0)\]
    • Check it is good. otherwise, replace \(x_0\) by \(x^{\star}\)

Newton algorithm (2)

  • Algorithm:
    • start with \(x_n\)
    • compute \(x_{n+1} = x_n- \frac{f(x_n)}{f^{\prime}(x_n)}=f^{\text{newton}}(x_n)\)
    • stop if \(|x_{n+1}-x_n|<\eta\) or \(|f(x_n)| < \epsilon\)
  • Convergence: quadratic

Quasi-Newton

  • What if we can’t compute \(f^{\prime}\) or it is expensive to do so?
    • Idea: try to approximate \(f^{\prime}(x_n)\) from the last iterates
  • Secant method: \[f^{\prime}(x_n)\approx \frac{f(x_n)-f(x_{n-1})}{x_n-x_{n-1}}\] \[x_{n+1} = x_n- f(x_n)\frac{x_n-x_{n-1}}{f(x_n)-f(x_{n-1})}\]
    • requires two initial guesses: \(x_1\) and \(x_0\)
    • superlinear convergence: \(\lim \frac{x_t-x^{\star}}{x_{t-1}-x^{\star}}\rightarrow 0\)

Limits of Newton’s method

  • How could Newton method fail?
    • bad guess
      • -> start with a better guess
    • overshoot
      • -> dampen the update (problem: much slower)
      • -> backtrack
    • stationary point
      • -> if root of multiplicity \(m\) try \(x_{n+1} = x_n- m \frac{f(x_n)}{f^{\prime}(x_n)}\)

(some graphs of failed Newton convergence)

Backtracking

  • Simple idea:
    • at stage \(n\) given \(f(x_n)\) compute Newton step \(\Delta_n=-\frac{f(x_n)}{f^{\prime}(x_n)}\)
    • find the smallest \(k\) such that \(|f(x_n-\Delta/2^k)|<|f(x_n)|\)
    • set \(x_{n+1}=x_n-\Delta/2^k\)

One dimensional minimization

Golden section search (2)

  • This is guaranteed to converge to a local minimum
  • In each step, the size of the interval is reduced by a factor \(\Phi\)
  • By choosing \(\Phi=\frac{\sqrt{5}-1}{2}\) one can save one evaluation by iteration.
    • you can check that either \(c_{n+1} = d_n\) or \(d_{n+1} = c_n\)
  • Remark that bisection is not enough

Gradient Descent

  • Minimize \(f(x)\) for \(x \in R\) given initial guess \(x_0\)
  • Algorithm:
    • start with \(x_n\)
    • compute \(x_{n+1} = x_n (1-\lambda)- \lambda f^{\prime}(x_n)\)
    • stop if \(|x_{n+1}-x_n|<\eta\) or \(|f^{\prime}(x_n)| < \epsilon\)

Gradient Descent (2)

  • Uses local information
    • one needs to compute the gradient
    • note that gradient at \(x_n\) does not provide a better guess for the minimum than \(x_n\) itself
    • learning speed is crucial
  • Convergence speed: linear
    • rate depend on the learning speed
    • optimal learning speed? the fastest for which there is convergence

Newton-Raphson method

  • Minimize \(f(x)\) for \(x \in R\) given initial guess \(x_0\)
  • Build a local model of \(f\) around \(x_0\) \[f(x) = f(x_0) + f^{\prime}(x_0)(x-x_0) + f^{\prime\prime}(x_0)\frac{(x-x_0)^2}{2} + o(x-x_0)^2\]
  • According to this model, \[ f(x{\star}) = min_x f(x)\iff \frac{d}{d x} \left[ f(x_0) + f^{\prime}(x_0)(x-x_0) + f^{\prime\prime}(x_0)\frac{(x-x_0)^2}{2} \right] = 0\] which yields: \(x^{\star} = x_0 - \frac{f^{\prime}(x_0)}{f^{\prime\prime}(x_0)}\)
  • this is Newton applied to \(f^{\prime}(x)=0\)

Newton-Raphson Algorithm (2)

  • Algorithm:
    • start with \(x_n\)
    • compute \(x_{n+1} = x_n-\frac{f^{\prime}(x_0)}{f^{\prime\prime}(x_0)}\)
    • stop if \(|x_{n+1}-x_n|<\eta\) or \(|f^{\prime}(x_n)| < \epsilon\)
  • Convergence: quadratic

Unconstrained Multidimensional Optimization

Unconstrained problems

  • Minimize \(f(x)\) for \(x \in R^n\) given initial guess \(x_0 \in R^n\)

  • Many intuitions from the 1d case, still apply

    • replace derivatives by gradient, jacobian and hessian
    • recall that matrix multiplication is not commutative

  • Some specific problems:

    • update speed can be specific to each dimension
    • saddle-point issues (for minimization)

Quick terminology

Function \(f: R^p \rightarrow R^q\)

  • Jacobian: \(J(x)\) or \(f^{\prime}\_x(x)\), \(p\times q\) matrix such that: \[J(x)\_{ij} = \frac{\partial f(x)\_i}{\partial x_j}\]

  • Gradient: \(\nabla f(x) = J(x)\), gradient when \(q=1\)

  • Hessian: denoted by \(H(x)\) or \(f^{\prime\prime}\_{xx}(x)\) when \(q=1\): \[H(x)\_{jk} = \frac{\partial f(x)}{\partial x_j\partial x_k}\]

  • In the following explanations, \(|x|\) denotes the supremum norm, but most of the following explanations also work with other norms.

Unconstrained Multidimensional Root-Finding

Multidimensional Newton-Raphson

  • Algorithm:
    • start with \(x_n\)
    • compute \(x_{n+1} = x_n- J(x_{n})^{-1}f(x_n)=f^{\text{newton}}(x_n)\)
    • stop if \(|x_{n+1}-x_n|<\eta\) or \(|f(x_n)| < \epsilon\)
  • Convergence: quadratic

Multidimensional Newton root-finding (2)

  • what matters is the computation of the step \(\Delta_n = {\color{\red}{J(x_{n})^{-1}}} f(x_n)\)
  • don’t compute \(J(x_n)^{-1}\)
    • it takes less operations to compute \(X\) in \(AX=Y\) than \(A^{-1}\) then \(A^{-1}Y\)
    • in Julia: X = A \ Y
  • strategies to improve convergence:
    • dampening: \(x_n = (1-\lambda)x_{n-1} - \lambda \Delta_n\)
    • backtracking: choose \(k\) such that \(|f(x_n-2^{-k}\Delta_n)|\)<\(|f(x_{n-1})|\)
    • linesearch: choose \(\lambda\in[0,1]\) so that \(|f(x_n-\lambda\Delta_n)|\) is minimal

Unconstrained Multidimensional Minimization

Multidimensional Gradient Descent

  • Minimize \(f(x) \in R\) for \(x \in R^n\) given \(x_0 \in R^n\)
  • Algorithm
    • start with \(x_n\) \[x_{n+1} = (1-\lambda) x_n - \lambda \nabla f(x_n)\]
    • stop if \(|x_{n+1}-x_n|<\eta\) or \(|f(x_n)| < \epsilon\)
  • Comments:
    • lots of variants
    • automatic differentiation software makes gradient easy to compute
    • convergence is typically linear

Gradient descent variants

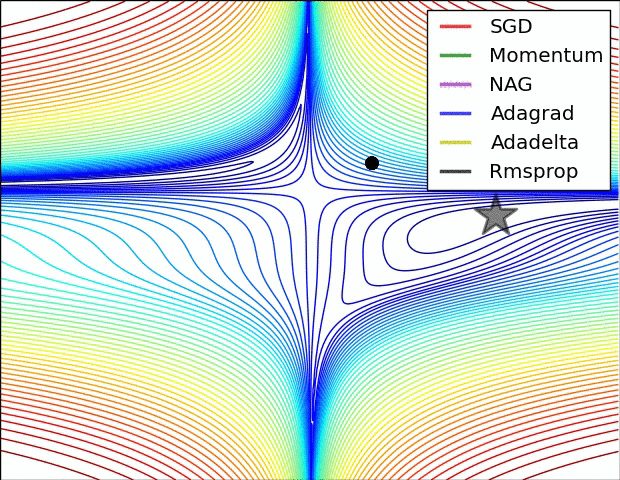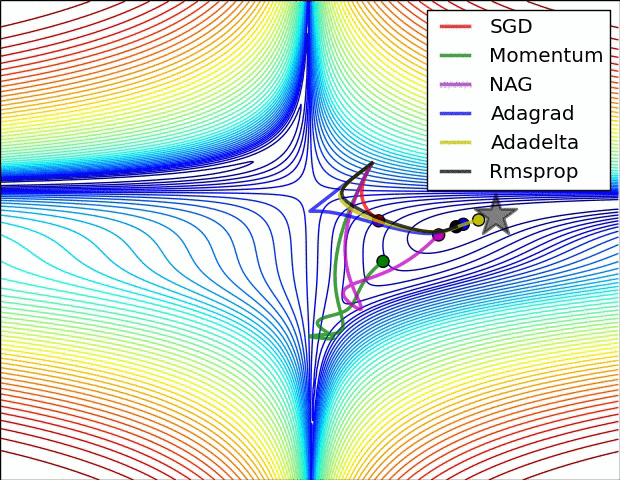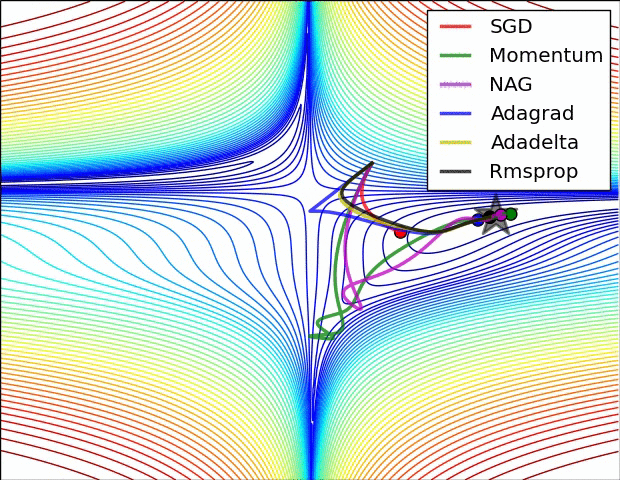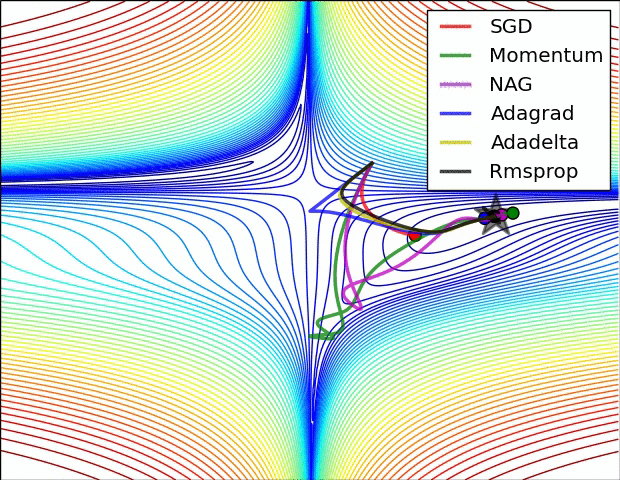
Multidimensional Newton Minimization

  • Algorithm:
    • start with \(x_n\)
    • compute \(x_{n+1} = x_n-{\color{\red}{H(x_{n})^{-1}}}\color{\green}{ J(x_n)'}\)
    • stop if \(|x_{n+1}-x_n|<\eta\) or \(|f(x_n)| < \epsilon\)
  • Convergence: quadratic
  • Problem:
    • \(H(x_{n})\) hard to compute efficiently
    • rather unstable

Quasi-Newton method for multidimensional minimization

  • Recall the secant method:
    • \(f(x_{n-1})\) and \(f(x_{n-2})\) are used to approximate \(f^{\prime}(x_{n-2})\).
    • Intuitively, \(n\) iterates would be needed to approximate a hessian of size \(n\)….
  • Broyden method: takes \(2 n\) steps to solve a linear problem of size \(n\)
    • uses past information incrementally

Quasi-Newton method for multidimensional minimization

  • Consider the approximation: \[f(x_n)-f(x_{n-1}) \approx J(x_n) (x_n - x_{n-1})\]
    • \(J(x_n)\) is unknown and cannot be determined directly as in the secant method.
    • idea: \(J(x_n)\) as close as possible to \(J(x_{n-1})\) while solving the secant equation
    • formula: \[J_n = J_{n-1} + \frac{(f(x_n)-f(x_{n-1})) - J_{n-1}(x_n-x_{n-1})}{||x_n-x_{n-1}||^2}(x_n-x_{n-1})^{\prime}\]

Gauss-Newton Minimization

  • Restrict to least-square minimization: $min_x _i f(x)_i^2 R $
  • Then up to first order, \(H(x_n)\approx J(x_n)^{\prime}J(x_n)\)
  • Use the step: \(({J(x_n)^{\prime}J(x_n)})^{-1}\color{\green}{ J(x_n)}\)
  • Convergence:
    • can be quadratic at best
    • linear in general

Levenberg-Marquardt

  • Least-square minimization: $min_x _i f(x)_i^2 R $

  • replace \({J(x_n)^{\prime}J(x_n)}^{-1}\) by \({J(x_n)^{\prime}J(x_n)}^{-1} +\mu I\)

    • adjust \(\lambda\) depending on progress

  • uses only gradient information like Gauss-Newton

  • equivalent to Gauss-Newton close to the solution (\(\mu\) small)

  • equivalent to Gradient far from solution (\(\mu\) high)

Constrained optimization and complementarity conditions

Consumption optimization

Consider the optimization problem: \[\max U(x_1, x_2)\]

under the constraint \(p_1 x_1 + p_2 x_2 \leq B\)

where \(U(.)\), \(p_1\), \(p_2\) and \(B\) are given.

How do you find a solution by hand?

Consumption optimization (1)

  • Compute by hand
  • Easy:
    • since the budget constraint must be binding, get rid of it by stating \(x_2 = B - p_1 x_1\)
    • then maximize in \(x_1\), \(U(x_1, B - p_1 x_1)\) using the first order conditions.
  • It works but:
    • breaks symmetry between the two goods
    • what if there are other constraints: \(x_1\geq \underline{x}\)?
    • what if constraints are not binding?
    • is there a better way to solve this problem?

Consumption optimization (2)

  • Another method, which keeps the symmetry. Constraint is binding, trying to minimize along the budget line yields an implicit relation between \(d x_1\) and \(d x_2\) \[p_1 d {x_1} + p_2 d {x_2} = 0\]
  • At the optimal: \(U^{\prime}\_{x_1}(x_1, x_2)d {x_1} + U^{\prime}\_{x_2}(x_1, x_2)d {x_2} = 0\)
  • Eliminate \(d {x_1}\) and \(d {x_2}\) to get one condition which characterizes optimal choices for all possible budgets. Combine with the budget constraint to get a second condition.

Penalty function

  • Take a penalty function \(p(x)\) such that \(p(x)=K>0\) if \(x>0\) and \(p(x)=0\) if \(x \leq 0\). Maximize: \(V(x_1, x_2) = U(x_1, x_2) - p( p_1 x_1 + p_2 x_2 - B)\)
  • Clearly, \(\min U \iff \min V\)
  • Problem: \(\nabla V\) is always equal to \(\nabla U\).
  • Solution: use a smooth solution function like \(p(x) = x^2\)
  • Problem: distorts optimization
    • Solution: adjust weight of barrier and minimize \(U(x_1, x_2) - \kappa p(x)\)
  • Possible but hard to choose the weights/constraints.

Penalty function

  • Another idea: is there a canonical way to choose \(\lambda\) such that at the minimum it is equivalent to minimize the original problem under constraint or to minimize \[V(x_1, x_2) = U(x_1, x_2) - \lambda (p_1 x_1 + p_2 x_2 - B)\]
  • Clearly, when the constraint is not binding we must have \(\lambda=0\). What should be the value of \(\lambda\) when the constraint is binding ?

Karush-Kuhn-Tucker conditions

  • If \((x^{\star},y^{\star})\) is optimal there exists \(\lambda\) such that:
    • \((x^{\star},y^{\star})\) maximizes lagrangian \(\mathcal{L} = U(x_1, x_2) + \lambda (B- p_1 x_1 - p_2 x_2)\)
    • \(\lambda \geq 0\)
    • \(B- p_1 x_1 - p_2 x_2 \geq 0\)
    • \(\lambda (B - p_1 x_1 - p_2 x_2 ) = 0\)
  • The three latest conditions are called “complementarity” or “slackness” conditions
    • they are equivalent to \(\min(\lambda, B - p_1 x_1 - p_2 x_2)=0\)
    • we denote \(\lambda \geq 0 \perp B- p_1 x_1 + p_2 x_2 \geq 0\)
  • \(\lambda\) can be interpreted as the welfare gain of relaxing the constraint.

Karush-Kuhn-Tucker conditions

  • We can get first order conditions that factor in the constraints:
    • \(U^{\prime}_x - \lambda p_1 = 0\)
    • \(U^{\prime}_y - \lambda p_2 = 0\)
    • \(\lambda \geq 0 \perp B-p_1 x_1 -p_2 x_2 \geq 0\)
  • It is now a nonlinear system of equations with complementarities (NCP)
    • there are specific solution methods to deal with it

Solution strategies for NCP problems

  • General formulation for vector-valued functions \[f(x)\geq 0 \perp g(x)\geq 0\] means \[\forall i, f_i(x)\geq 0 \perp g_i(x)\geq 0\]

    • NCP do not necessarily arise from a single optimization problem

  • There are robust (commercial) solvers for NCP problems (PATH, Knitro) for that

  • How do we solve it numerically?

    • assume constraint is binding then non-binding then check which one is good
      • OK if not too many constraints
    • reformulate it as a smooth problem
    • approximate the system by a series of linear complementarities problems (LCP)

Smooth method

  • Consider the Fisher-Burmeister function \[\phi(a,b) = a+b-\sqrt{a^2+b^2}\]
  • It is infinitely differentiable, except at \((0,0)\)
  • Show that \(\phi(a,b) = 0 \iff \min(a,b)=0 \iff a\geq 0 \perp b \geq 0\)
  • After substitution in the original system one can use regular non-linear solver
    • fun fact: the formulation with a \(\min\) is nonsmooth but also works quite often

Practicalities

Optimization libraries

  • Robust optimization code is contained in the following libraries:
    • Roots.jl: one-dimensional root finding
    • NLSolve.jl: multidimensional root finding (+complementarities)
    • Optim.jl: minimization
  • The two latter libraries have a somewhat peculiar API, but it’s worth absorbing it.
    • in particular they provide non-allocating algorithms for functions that modify arguments in place
    • they are compatible with automatic differentiation
julia> f(x) = [x[1] - x[2] - 1, x[1] + x[2]]
f (generic function with 1 method)

julia> NLsolve.nlsolve(f, [0., 0.0])
Results of Nonlinear Solver Algorithm
 * Algorithm: Trust-region with dogleg and autoscaling
 * Starting Point: [0.0, 0.0]
 * Zero: [0.5000000000009869, -0.5000000000009869]
 * Inf-norm of residuals: 0.000000       
 * Iterations: 1                       
 * Convergence: true
   * |x - x'| < 0.0e+00: false
   * |f(x)| < 1.0e-08: true                           
 * Function Calls (f): 2
 * Jacobian Calls (df/dx): 2